中学受験理科講座 電流と抵抗
電流と抵抗 解説動画
電流と抵抗 一問一答プリントはこちらをクリック
中学受験理科 オンラインテストはこちらをクリック
抵抗と豆電球
「抵抗」の意味
Haru_You
金属は電気を通しやすく、ゴムやプラスチックは電気を通しにくいのはわかるよね。
この「電気を通しにくくするはたらき」のことを電気抵抗というんだ。
省略して抵抗、とよぶことが多いけどね。
この「電気を通しにくくするはたらき」のことを電気抵抗というんだ。
省略して抵抗、とよぶことが多いけどね。
通しやすくするはたらきじゃなくて、通しにくくするほうに注目するのはなんで?
はるか
Haru_You
銅や銀みたいに、電気が通りやすいものは回路につないだときに電流をそのまま流す導線になっちゃうんだ。
けど、抵抗が大きいものは、電気を通すときに電気のエネルギーを熱や光に変える性質があるんだよ。
けど、抵抗が大きいものは、電気を通すときに電気のエネルギーを熱や光に変える性質があるんだよ。
抵抗があるから、電気を光や熱のエネルギーとして利用できるんだね。
だから通しにくくするはたらき、抵抗に注目するってことか。
だから通しにくくするはたらき、抵抗に注目するってことか。
はるか
豆電球のフィラメント
Haru_You
たとえば豆電球が光るはたらきについて考えてみようか。
豆電球の発光部分のフィラメントにはタングステンという金属が使われているんだ。
豆電球の発光部分のフィラメントにはタングステンという金属が使われているんだ。
そのタングステンっていう金属は、抵抗が大きいから光るってこと？
はるか
Haru_You
うん、タングステンは導線部分より抵抗が大きくて、電流が流れるときにエネルギーが光に変わりやすい性質を持っているんだよ。
ただ、光だけでなく熱も発生させるから、フィラメントが燃えないように豆電球のガラス球内部は真空にしたり、ちっ素やアルゴンなどの不燃性ガスを詰めてあるんだ。
ただ、光だけでなく熱も発生させるから、フィラメントが燃えないように豆電球のガラス球内部は真空にしたり、ちっ素やアルゴンなどの不燃性ガスを詰めてあるんだ。
そういえば、エジソンが作った電球ではフィラメントに京都の竹を使ったけどすぐに燃えちゃったんだっけ。
そんなに大きな熱が発生するんだね。
そんなに大きな熱が発生するんだね。
はるか
Haru_You
電気ストーブとかあるじゃん。
あれの抵抗にはニッケルとクロムという2種類の金属による合金のニクロムが使われているんだけど、ニクロムは電気のエネルギーを熱に変えやすいんだ。
あれの抵抗にはニッケルとクロムという2種類の金属による合金のニクロムが使われているんだけど、ニクロムは電気のエネルギーを熱に変えやすいんだ。
電流計のつなぎかた
電流の大きさ
抵抗によって電気の通りやすさが変わるのはわかったけど、それを数字で測ることはできないの？
はるか
Haru_You
回路にどれくらい電気が通るかを表したものが電流の大きさで、電流を測るには電流計という器具を使うんだ。
電流の大きさはA（アンペア）という単位だけど、乾電池と豆電球で実験するときにはmA（ミリアンペア）という単位で求めることが多いね。
電流の大きさはA（アンペア）という単位だけど、乾電池と豆電球で実験するときにはmA（ミリアンペア）という単位で求めることが多いね。
ミリってことは、mgやmLと同じように使うのかな。
はるか
Haru_You
そうだね、「ミリ」は$\frac{1}{1000}$、という意味の接頭辞だから、1000mAで1Aになるよ。
電流計のつなぎかた
電流計を回路の中につなげば電流の大きさが測れるんだね。
はるか
Haru_You
そうなんだけど、電流計はつなぎ方に注意しないといけないんだよ。
電流を測りたい抵抗の場所に対して、枝分かれせず直列に電流計をつながないといけないんだ。
電流を測りたい抵抗の場所に対して、枝分かれせず直列に電流計をつながないといけないんだ。
なんで?
はるか
Haru_You
並列に分かれた回路には、別々の電流が流れ込むからね。
で、電流計自体は抵抗にならないから、電流計をつないだ部分に大きな電流が流れて、壊れてしまうんだよ。
で、電流計自体は抵抗にならないから、電流計をつないだ部分に大きな電流が流れて、壊れてしまうんだよ。
電流計の読み方
電流計に、導線をつなぐ端子が4個あるのはどう使うの?
はるか
Haru_You
赤い端子が+端子で、電池の+極側につなぐんだ。
いっぽう、3つある黒い端子が－端子で、それぞれ電流の大きさに応じてつなぎ替えるんだ。
いっぽう、3つある黒い端子が－端子で、それぞれ電流の大きさに応じてつなぎ替えるんだ。
でもさ、電流の大きさがわからないから電流計につなぐのに、電流の大きさに合わせてつなぎ替えるって無理じゃない?
はるか
Haru_You
うん、だから最初は一番大きな電流を測る5A端子につなぐんだ。
で、針の動きがほとんどなかったら小さい電流が流れていることになるから、500mAや50mAの端子につなぎ替えるんだ。
50mAの端子につないだときに大きな電流が流れると、やはり電流計が壊れてしまうんだよ。
で、針の動きがほとんどなかったら小さい電流が流れていることになるから、500mAや50mAの端子につなぎ替えるんだ。
50mAの端子につないだときに大きな電流が流れると、やはり電流計が壊れてしまうんだよ。
すると、電流計の針を読むときはどの端子につないだかを考えないといけないんだね。
はるか
Haru_You
図では針が2.8Aの位置にあるけど、これは5A端子につないでいれば2.8Aって読むってことだね。
もし500mA端子につないであるなら280mAをさしていることになるし、50mA端子につないであれば28mAをさしていることになるんだ。
もし500mA端子につないであるなら280mAをさしていることになるし、50mA端子につないであれば28mAをさしていることになるんだ。
豆電球の直列つなぎ
直列つなぎの意味
何回か出てきた言葉だけど、直列つなぎってどんなつなぎかただっけ？
はるか
Haru_You
途中で枝分かれせず、抵抗が一直線に列をつくるのが直列つなぎだね。
回路全体だけでなく「豆電球が直列」「乾電池が直列」みたいに部分的に見ることもあるからね。
回路全体だけでなく「豆電球が直列」「乾電池が直列」みたいに部分的に見ることもあるからね。
直列つなぎでは、1本の道を電流が流れるってことだね。
そしたら、抵抗を通るたびに電気が使われて、電流が小さくなっていくのかな?
そしたら、抵抗を通るたびに電気が使われて、電流が小さくなっていくのかな?
はるか
Haru_You
いや、抵抗で電気が使われて減るって考え方をしちゃいけないんだ。
抵抗で使われる量に合わせて電流が送り出されるので、直列につながった回路の中では、流れる電流の大きさはどこも同じになるんだよ。
抵抗で使われる量に合わせて電流が送り出されるので、直列につながった回路の中では、流れる電流の大きさはどこも同じになるんだよ。
1本の道だから、どこにも同じ電流が流れているって考えればいいのね。
はるか
抵抗の計算
豆電球を直列つなぎにしたときって豆電球が暗くなったよね。
あれはどうして?
あれはどうして?
はるか
Haru_You
豆電球を直列につなぐと、抵抗が大きくなって電流が小さくなるから、豆電球が暗くなるんだ。
抵抗のことを電流が通りにくい細い道だと考えると、豆電球が2個直列になったら細い道の長さが2倍になるよね。
そしたら、電流が通り抜けるのにかかる時間も2倍になるから、同じ時間で回路を通れる電流は半分になり、明るさも半分になるってことなんだ。
抵抗のことを電流が通りにくい細い道だと考えると、豆電球が2個直列になったら細い道の長さが2倍になるよね。
そしたら、電流が通り抜けるのにかかる時間も2倍になるから、同じ時間で回路を通れる電流は半分になり、明るさも半分になるってことなんだ。
てことは、豆電球3個直列だと、電流の大きさと豆電球の明るさは$\frac{1}{3}$になるってことかな。
はるか
Haru_You
その通り。
豆電球1個の抵抗を1、豆電球1個に乾電池1個をつないだときの電流の大きさ（明るさ）を1とするよ。
このとき、豆電球を直列に2個、3個･･･と増やしていくと回路全体の抵抗が2、3･･･と大きくなり、回路を流れる電流と豆電球の明るさは$\frac{1}{2}$、$\frac{1}{3}$･･･となっていくんだ。
この計算の考え方はあとでまた使うから覚えておいてね。
豆電球1個の抵抗を1、豆電球1個に乾電池1個をつないだときの電流の大きさ（明るさ）を1とするよ。
このとき、豆電球を直列に2個、3個･･･と増やしていくと回路全体の抵抗が2、3･･･と大きくなり、回路を流れる電流と豆電球の明るさは$\frac{1}{2}$、$\frac{1}{3}$･･･となっていくんだ。
この計算の考え方はあとでまた使うから覚えておいてね。
直列につないだ豆電球の性質
Haru_You
豆電球が直列につないである回路で、そのうちの1個の豆電球を外したり、1個が切れてしまったりしたらどうなると思う?
抵抗の数が減るから、電流が大きくなって豆電球が明るくなるのかな?
はるか
Haru_You
いや、直列の豆電球を1つ外したら、そこで回路がとぎれるから、電流が流れなくなって豆電球も全て消えるんだ。
そっか。
じゃあさ、豆電球の直列つなぎって暗くなるし、1つ外したら全部消えちゃうしで、何もいいことなくない?
じゃあさ、豆電球の直列つなぎって暗くなるし、1つ外したら全部消えちゃうしで、何もいいことなくない?
はるか
Haru_You
ところがね、豆電球が直列つなぎだと、回路全体を流れる電流が小さくなるから、乾電池が長持ちするという利点があるんだよ。
豆電球の並列つなぎ
並列つなぎの意味
Haru_You
直列つなぎに対して、導線が枝分かれして、複数の通り道ができる回路が並列つなぎだね。
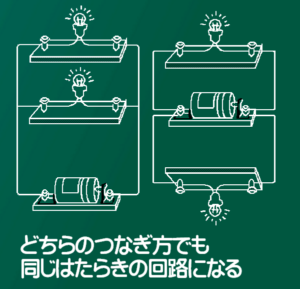
並列つなぎって、はじめから2本別々の導線が乾電池につながるのと、導線の途中から分かれるのとがあるよね。
あれはどう違うの?
あれはどう違うの?
はるか
Haru_You
うん、実はその2つの回路はまったく同じ意味になるんだ。
並列つなぎでは、枝分かれした道の1つ1つを別々の回路として考えることができるんだよ。
並列つなぎでは、枝分かれした道の1つ1つを別々の回路として考えることができるんだよ。
並列豆電球の抵抗計算
豆電球を2個並列につないだ回路では、それぞれ豆電球が1個だけつながった回路が2つあると考えればいいってことかな?
はるか
Haru_You
そうだね。
だから、並列につないだ豆電球は、豆電球を1個だけつないだときと同じ明るさになるんだよ。
それぞれの豆電球に1の電流が流れるから、明るさも1になるんだ。
だから、並列につないだ豆電球は、豆電球を1個だけつないだときと同じ明るさになるんだよ。
それぞれの豆電球に1の電流が流れるから、明るさも1になるんだ。
じゃあ、それぞれの豆電球に1の電流が流れるんだと、枝分かれした道が1つにまとまるところでは電流が2になるの?
はるか
Haru_You
うん、並列回路では部分ごとの電流を計算して、その合計が全体の電流になるんだよ。
たとえば豆電球を1個ずつ、3個並列につないだ回路では部分ごとに1ごとの電流が流れ、全体の電流は3になるんだ。
たとえば豆電球を1個ずつ、3個並列につないだ回路では部分ごとに1ごとの電流が流れ、全体の電流は3になるんだ。
電流が大きくなるということは、並列に豆電球をつなぐと抵抗が小さくなるってこと?
はるか
Haru_You
うん、並列につなぐってことは電流の通り道が増えるってことだから、抵抗が小さくなるんだよ。
並列回路では先に全体の電流を計算したあと、その逆数を回路全体の抵抗にするんだ。
この計算もあとで使うから覚えておいてね。
並列回路では先に全体の電流を計算したあと、その逆数を回路全体の抵抗にするんだ。
この計算もあとで使うから覚えておいてね。
並列豆電球の性質
Haru_You
豆電球を並列につなぐと、何個でも同じ明るさで豆電球を光らせることができるんだけど、乾電池が早く切れてしまうという欠点があるんだ。
そっか、回路全体の電流が大きくなるってことは、乾電池から多くの電流が流れるってことだもんね。
はるか
Haru_You
あと、並列につないだ豆電球のうち1個を外したらどうなるかわかるかい?
別々の回路として考えればいいんだから、他の豆電球に影響はないんじゃないかな。
はるか
Haru_You
正解。
並列につないだ豆電球の1個を外したり切れたりしても、他の導線を通る豆電球は明るさを変えずについたままになるんだ。
並列につないだ豆電球の1個を外したり切れたりしても、他の導線を通る豆電球は明るさを変えずについたままになるんだ。
豆電球の直並列つなぎ
並列部分に直列がはいる場合
Haru_You
1つの回路に直列つなぎと並列つなぎの両方があるつなぎ方を直並列つなぎというんだけど、直並列つなぎにも2種類あるんだ。
まずは回路全体で導線が枝分かれして、並列になったそれぞれの部分で豆電球が直列になっている場合から考えよう。
まずは回路全体で導線が枝分かれして、並列になったそれぞれの部分で豆電球が直列になっている場合から考えよう。
逆にいうと、枝分かれしていない部分には、豆電球がない場合ってことだね。
はるか
Haru_You
うん、抵抗が並列に枝分かれした先にしかなければ、それぞれ別々に電流を計算すればいいことになるからね。
まず図1を見てごらん。
まず図1を見てごらん。
豆電球2個直列の回路と、豆電球1個の回路が並列につながってる回路だね。
はるか
Haru_You
この場合、上側の豆電球2個直列の回路は抵抗が2、すなわち電流$\frac{1}{2}$が流れる。
また、下の豆電球1個の回路は抵抗が1、だから1の電流が流れるって考えられるね。
このとき、回路全体を流れる電流は部分ごとの電流の合計、（$\frac{1}{2}$+1＝）$\frac{3}{2}$になるんだよ。
また、下の豆電球1個の回路は抵抗が1、だから1の電流が流れるって考えられるね。
このとき、回路全体を流れる電流は部分ごとの電流の合計、（$\frac{1}{2}$+1＝）$\frac{3}{2}$になるんだよ。
てことは、下の豆電球はふつうに電池につないだときの明るさで、上の豆電球2つは下の豆電球の2分の1の明るさになってるんだね。
はるか
Haru_You
図2なら上が$\frac{1}{2}$、下が$\frac{1}{3}$の電流が流れて、全体で（$\frac{1}{2}$＋$\frac{1}{3}$＝）$\frac{5}{6}$の電流が流れている、ってのもわかるよね。
並列部分が他の抵抗と直列になる場合
Haru_You
直並列回路では、並列になった部分が、他の抵抗と直列になるつなぎ方もあるんだ。
この場合にはさっき説明した直列・並列それぞれの抵抗の考え方を使って、部分ごとの抵抗の和を全体抵抗にして、その逆数を回路全体の電流にするんだ。
この場合にはさっき説明した直列・並列それぞれの抵抗の考え方を使って、部分ごとの抵抗の和を全体抵抗にして、その逆数を回路全体の電流にするんだ。
えーと、直列になってる1つ1つの豆電球の抵抗はそれぞれが1。
並列になっている部分の抵抗は、豆電球の数に合わせて$\frac{1}{2}$、$\frac{1}{3}$･･･だったよね。
並列になっている部分の抵抗は、豆電球の数に合わせて$\frac{1}{2}$、$\frac{1}{3}$･･･だったよね。
はるか
Haru_You
うん、まずは図3を見てごらん。
豆電球を1個ずつ並列にした右の部分が、左の豆電球1個と直列につながれているよね。
豆電球を1個ずつ並列にした右の部分が、左の豆電球1個と直列につながれているよね。
この場合、左の豆電球には右の2個の豆電球を流れた電流が合わせて流れ込むんだから、左のほうが明るく光るんだよね。
左の豆電球は抵抗1で、右の豆電球は2個並列だから、部分抵抗が$\frac{1}{2}$になるって考えればいいのかな?
左の豆電球は抵抗1で、右の豆電球は2個並列だから、部分抵抗が$\frac{1}{2}$になるって考えればいいのかな?
はるか
Haru_You
うん、正解。
そうしたら左と右は直列だから、回路全体の抵抗は合計して（1+$\frac{1}{2}$＝）$\frac{3}{2}$になるよね。
この回路全体の抵抗の逆数が、回路全体の電流になるから、$\frac{2}{3}$の電流が流れるとわかるんだよ。
で、ここの並列部分は上下で同じ回路で電流が半分ずつに分かれるから、それぞれ$\frac{1}{3}$の電流が流れるんだ。
そうしたら左と右は直列だから、回路全体の抵抗は合計して（1+$\frac{1}{2}$＝）$\frac{3}{2}$になるよね。
この回路全体の抵抗の逆数が、回路全体の電流になるから、$\frac{2}{3}$の電流が流れるとわかるんだよ。
で、ここの並列部分は上下で同じ回路で電流が半分ずつに分かれるから、それぞれ$\frac{1}{3}$の電流が流れるんだ。
じゃあ、もし豆電球が直列に2個と、並列部分が3個並列だったら抵抗が（１＋１＋$\frac{1}{3}$＝）$\frac{7}{3}$で、全体の電流が$\frac{3}{7}$ってやればいいんだね。
ルールさえ覚えておければできそうだな。
ルールさえ覚えておければできそうだな。
はるか
Haru_You
実際にテストに出る問題の大半は、この全体電流が$\frac{2}{3}$になる1個-2個の直並列だから、まずはこれだけやり方を覚えてくれればいいよ。
あと、この回路が問題になったとき必ず聞かれるのが、豆電球を1個外したときの明るさの変化だ。
あと、この回路が問題になったとき必ず聞かれるのが、豆電球を1個外したときの明るさの変化だ。
左の1個をはずすと、直列の回路がとぎれるから全部消えるよね。
右側の並列部分から1個外すと･･･ただの2個直列つなぎになるってことかな。
右側の並列部分から1個外すと･･･ただの2個直列つなぎになるってことかな。
はるか
Haru_You
うん、そうすると流れる電流は2分の1になるよね。
もともとは$\frac{2}{3}$の電流が流れていた左の豆電球は暗くなり、右側の並列部で残った豆電球は電流が$\frac{1}{3}$だったのが$\frac{1}{2}$になるから、少し明るくなるんだ。
もともとは$\frac{2}{3}$の電流が流れていた左の豆電球は暗くなり、右側の並列部で残った豆電球は電流が$\frac{1}{3}$だったのが$\frac{1}{2}$になるから、少し明るくなるんだ。
複雑な直並列回路
Haru_You
直並列つなぎをさらに複雑にすると、他の豆電球と直列に、直並列の部分が入ってくる形になるんだ。
たとえば図4みたいな回路図だね。
たとえば図4みたいな回路図だね。
でも、豆電球1個の部分は抵抗1なんだから、一番右の直並列部分の部分抵抗さえわかれば求められるよね。
はるか
Haru_You
そうだね。
そこだけ独立して考えてみると、これは図1と同じ回路だよね。
そこだけ独立して考えてみると、これは図1と同じ回路だよね。
たしかに。
これは電流が$\frac{2}{3}$流れる回路だったね。
これは電流が$\frac{2}{3}$流れる回路だったね。
はるか
Haru_You
だからその部分の抵抗は、電流の逆数$\frac{3}{2}$と考えて計算すればいいんだよ。
そうすれば全体の抵抗は$\frac{8}{3}$になるから、電流も計算できるね。
はるか
Haru_You
こんな風に、複雑な直並列つなぎでは直列になった各部分の抵抗について、独立した回路にしたときの抵抗をあてはめていく必要があるんだ。
まあ、最近はあまり入試で見ないんだけどね、これ。
まあ、最近はあまり入試で見ないんだけどね、これ。
乾電池のつなぎかた
乾電池の直列つなぎ
Haru_You
抵抗のつなぎかただけじゃなく、乾電池のつなぎかたにも直列と並列で違いがあるんだよ。
ふつうに電池2個をつなぐと、＋極と－極をくっつける直列つなぎになるよね。
そしたら、豆電球が明るくなるんだから、電流も大きくなったるんだよね。
そしたら、豆電球が明るくなるんだから、電流も大きくなったるんだよね。
はるか
Haru_You
うん、乾電池を2個、3個･･･と直列つなぎにすると電流が2倍、3倍･･･と大きくなるから、豆電球が明るくなるんだよ。
そのかわり、直列つなぎにした乾電池は早く寿命が切れてしまうんだ。
そのかわり、直列つなぎにした乾電池は早く寿命が切れてしまうんだ。
なんで?
乾電池1個ずつが、電流を1ずつ出して合計2になるんだから、乾電池1個あたりの電流の量は乾電池1個のときと同じじゃないの?
乾電池1個ずつが、電流を1ずつ出して合計2になるんだから、乾電池1個あたりの電流の量は乾電池1個のときと同じじゃないの?
はるか
Haru_You
直列回路は回路全体に同じ電流を流すから、豆電球の電流が2なら乾電池1個あたりの電流も2になるんだと思っておいて。
電圧という要素が関係しているんだけど、中学受験の理科ではそこを扱わないんだよね。
電圧という要素が関係しているんだけど、中学受験の理科ではそこを扱わないんだよね。
乾電池の並列つなぎ
Haru_You
いっぽう、乾電池を並列つなぎにした場合だけど、乾電池1個のときと回路全体の電流量（豆電球の明るさ）は変わらないんだ。
乾電池を並列につなぐって、どんなつなぎ方になるの?
はるか
Haru_You
乾電池の+極どうし、－極どうしを導線でむすび、それぞれの導線から抵抗につながる導線を伸ばすんだよ。
回路図を見ておいてね。
回路図を見ておいてね。
乾電池が2つあるのに回路全体の電流が変わらないってことは、乾電池1個あたりの電流は小さくなっているのかな？
はるか
Haru_You
そうだね、並列に乾電池を2個、3個･･･とつないだときは、1個あたりの電流量は$\frac{1}{2}$、$\frac{1}{3}$･･･になるから、結果として乾電池が長持ちするんだ。
直列と並列のまとめ
直列と並列のちがいと使い方
Haru_You
いろいろ説明したけど、要するに、並列つなぎでは電流（明るさ）は変わらず、直列つなぎでは電流（明るさ）が変わるってだけなんだよね。
たくさん回路図が出てきて、一番明るいのを選びなさいとか、もとの回路と同じ明るさのを選びなさい、とか聞かれたときにはそうやって考えればいいってことね。
はるか
Haru_You
あと、豆電球1個・乾電池1個の基本回路の電流が指定されていて、回路ごとや部分ごとの電流を聞かれた場合は、直列部分につないだ数で比例計算すればいいんだよ。
えーと、じゃあ基本の回路の電流が120mAで、乾電池3個直列、豆電球4個直列の回路の電流はいくつになるかな?
はるか
Haru_You
電池で3倍、豆電球で$\frac{1}{4}$だから、120×3÷4＝90mAだね。
計算の理屈さえ覚えれば、これは簡単だよ。
計算の理屈さえ覚えれば、これは簡単だよ。
スイッチのある回路
回路のショート
Haru_You
最後に、スイッチのある回路について。
基本的には、スイッチが入ったところがつながるように、指で一周してみればどんなつながりになっているかわかるよ。
基本的には、スイッチが入ったところがつながるように、指で一周してみればどんなつながりになっているかわかるよ。
図の回路だと、アを入れると上の導線で豆電球Bが、イを入れるとAとBが、ウを入れるとAとCがつながる形になるね。
はるか
Haru_You
ここで注意しないといけないのが、アとイを同時に入れたときなんだ。
上からBに、下からAとBにつながるんじゃないの?
はるか
Haru_You
たしかに導線は上下ともつながっているけど、全て上の導線に流れて、下の導線と豆電球Aには電流は流れないんだよ。
この現象をショートというんだ。
この現象をショートというんだ。
ショートって、壊れてつかなくなることじゃないの?
はるか
Haru_You
いや、ショートというのは「近道」という意味でね。
電流が分かれ道を通るとき、抵抗のない導線があれば全てそちらに流れてしまうことがショートなんだ。回路の中で1個しかない抵抗をショートしちゃうと、電池から出た電流がそのまま電池に戻ってしまい、発熱など器具が壊れる原因になるからね。
電流が分かれ道を通るとき、抵抗のない導線があれば全てそちらに流れてしまうことがショートなんだ。回路の中で1個しかない抵抗をショートしちゃうと、電池から出た電流がそのまま電池に戻ってしまい、発熱など器具が壊れる原因になるからね。
この場合、Aの豆電球がショートされてもBの豆電球が抵抗になるから、ショートしても壊れるわけじゃないんだね。
はるか
階段の上下で電灯をつけるスイッチ
Haru_You
家の階段や、廊下の両端なんかでは、どちらからでも電灯をオンオフできるスイッチがあるだろ。
あれ、どういう回路図になるかわかるかい？
あれ、どういう回路図になるかわかるかい？
消えてるときにスイッチを動かすと、どっちのスイッチを入れてもつくし、ついてるときにスイッチを動かすと、やっぱりどっちのスイッチでも切れるやつだね。
言われて見ると、不思議な回路だなあ。
言われて見ると、不思議な回路だなあ。
はるか
Haru_You
２つのスイッチを並列に並べればいいんだけど、実際に取り上げられた入試問題があるから、ちょっと確認してみてね。
https://haruyou-blog.com/2019/05/19/post-5000/電流と抵抗 まとめ
・電気を通しにくくするはたらきを抵抗という
・豆電球のフィラメントに用いられるタングステンという金属は抵抗が大きく、電気が通るときに電気を光のエネルギーに変える
・電流の単位はアンペア（A）で、電流計は回路の中に直列につなぐ
・豆電球を直列に2個、3個･･･つなぐと抵抗が2倍、3倍･･･になり、電流（明るさ）は$\frac{1}{2}$、$\frac{1}{3}$･･･になる
・豆電球を並列に2個、3個･･･つないでも、それぞれの電流（明るさ）・抵抗は豆電球1個をつないだときと同じで、回路全体では電流が2倍、3倍･･･になり、抵抗は$\frac{1}{2}$、$\frac{1}{3}$･･･になる
・乾電池を直列につなぐと回路全体を流れる電流が大きくなり、乾電池を並列につなぐと回路全体を流れる電流の大きさは変わらないが、乾電池1個あたりの電流が小さくなり、電池が長持ちする
・並列に枝分かれする回路で、抵抗のない導線にすべての電流が流れてしまうことをショートという
電流と抵抗 一問一答演習問題プリント
演習プリントには、Excelファイル版とPDFファイル版があります。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
なお、PDF版では20問の収録ですが、Excel版にはより多くの問題を収録しています。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
なお、PDF版では20問の収録ですが、Excel版にはより多くの問題を収録しています。
はるか
電流と抵抗（PDF版）
1 ファイル 455.61 KB
利用規定です。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
はるか
新着記事
都立中高一貫校のHPで公開されている適性検査問題の作文（適性検査Ⅰ）を1つのPD ...
社会科、日本の歴史の各時代の重要事項を「アルプス一万尺」に乗せて歌います。。
中学受験理科講座 植物のつくりとはたらき(3)〜光合成・呼吸・蒸散〜
理科の生物範囲、植物のつくりとはたらきについて、光合成・呼吸・蒸散のはたらきにつ ...
中学受験で頻出の11種類の水溶液の名前、液性、指示薬の変化、主な水溶液の識別ポイ ...
コロナウイルスの影響で、中学受験の学習塾業界にも営業自粛要請が出ています。この状 ...