2人の距離のグラフ（聖光学院　H24大問5）

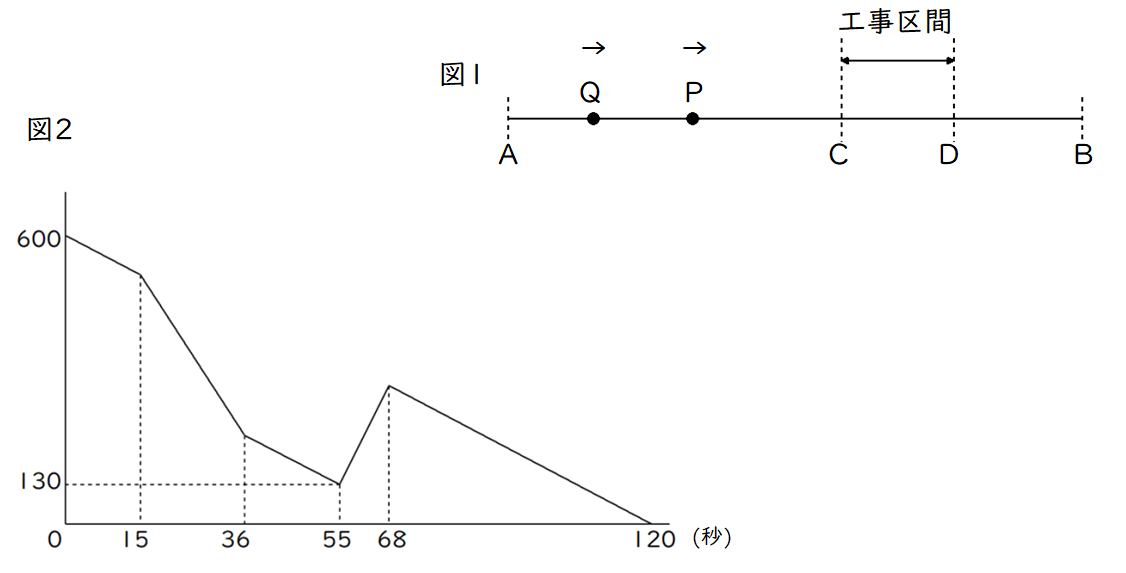
高速道路上を2台の車P、Qが走っていて、QがPを後ろから追いかけています。QにはPとの距離を測定する機械がついていて、QがA地点を通過したとき、2台の車の距離は600mでした。また、QがPに追いついた場所をB地点とします。A地点とB地点の途中のC地点とD地点の間は、工事区間のため、2台ともそれ以外の区間の【ア】倍の速さで走行します。QはA地点を通過してから、ちょうど2分後にB地点を通過しました。図2は、QがA地点を通過してからB地点を通過するまでの2台の車の距離と時間の関係を表したグラフです。このとき、次の問いに答えなさい。ただし、A地点とB地点の間の道路は直線であり、2台の車はC地点とD地点を通過するとき以外は、速さを変えないものとします。また、車の大きさは考えないものとします。

(1)Qが工事区間を通過するのに何秒かかりましたか。
(2)工事区間を走ったときのPとQの速さの比を最も簡単な整数比で答えなさい。
(3)Qが工事区間以外を走ったときの速さは毎秒何mですか。
(4)【ア】にあてはまる数を求めなさい。

解法のポイント

折りたたみ可能コンテンツ

ダイヤグラムの読み取りでは「グラフの折れ曲がり点」に注目するのが鉄則です。（1）（2）ではダイヤグラム上の600m、130mは使わないことに注意。
問題文の条件より、グラフが折れ曲がる（移動のしかたが変わる）のは工事区間に入るときだけですから、4回の折れ曲がりにそれぞれPとQがC、Dを通過するときのいずれかをあてはめます。
（1）はグラフを読むだけ、（2）は（1）と同様にPの工事区間通過時間を求め、速さと時間の逆比で解けます。
2台とも工事区間の速さはもとの速さの【ア】倍ですから、工事区間の速さの比＝もとの速さの比になります。QがAC間を通過するのにかかる時間はグラフから読み取れますから、PがAC間を通過する時間もわかります。これより、QがA地点を通過したときの600m差（PがA地点から600m進んでいる）に何秒かかるかで、（3）が求められます。
（4）は55秒のときの130mと、次の68秒の意味を考えましょう。（3）の解答と組み合わせればすぐに解けます。