立方体の展開図(国学院久我山ST H24 大問3)
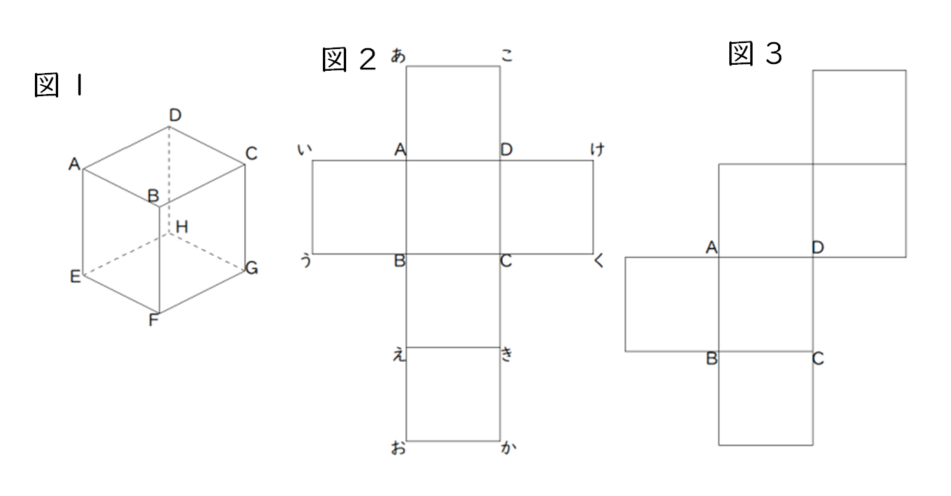
図1のような立方体ABCD-EFGHがあります。図2、図3はこの立方体の展開図です。次の問に答えなさい。
(1)図2の展開図で、図1の点Gに当たる点をあ~この中からすべて選びなさい。
(2)図1の辺EFを3等分する点のうちEに近い点をP、辺EHを3等分する点のうちEに近い点をQとします。3点B、P、Qを通る平面でこの立方体を切ったときにできる切り口の線を図2、図3に書き入れなさい。
(3)(2)の図3に書き入れた線で図3の展開図を切ると、5つの図形に分かれます。その中で1番大きい図形の面積は何cm2ですか。ただし、この立方体の1つの面の対角線の長さは6cmです。

(1)図2の展開図で、図1の点Gに当たる点をあ~この中からすべて選びなさい。
(2)図1の辺EFを3等分する点のうちEに近い点をP、辺EHを3等分する点のうちEに近い点をQとします。3点B、P、Qを通る平面でこの立方体を切ったときにできる切り口の線を図2、図3に書き入れなさい。
(3)(2)の図3に書き入れた線で図3の展開図を切ると、5つの図形に分かれます。その中で1番大きい図形の面積は何cm2ですか。ただし、この立方体の1つの面の対角線の長さは6cmです。
解法のポイント
(1)は立方体の展開図の頂点を決める問題です。
「立方体上で対角線の位置にある頂点は展開図で正方形を2枚並べた長方形の対角線」と、「L字に折れ曲がる角をはさむように同じ頂点」の2つを理解していればすぐに決まるでしょう。
(2)は切断面を展開図にしますが、面が台形(四角形)になるので、4本の線を引くことさえわかれば(1)と同様に頂点を決めて書けます。
(3)は展開図上の一部分の面積を求めます。「対角線の長さ」が与えられていますが、正方形の面積は「対角線×対角線÷2」で求められることと、相似(面積比)のルールを使って一枚ずつ面積を求めていくといいでしょう。
解答・解説
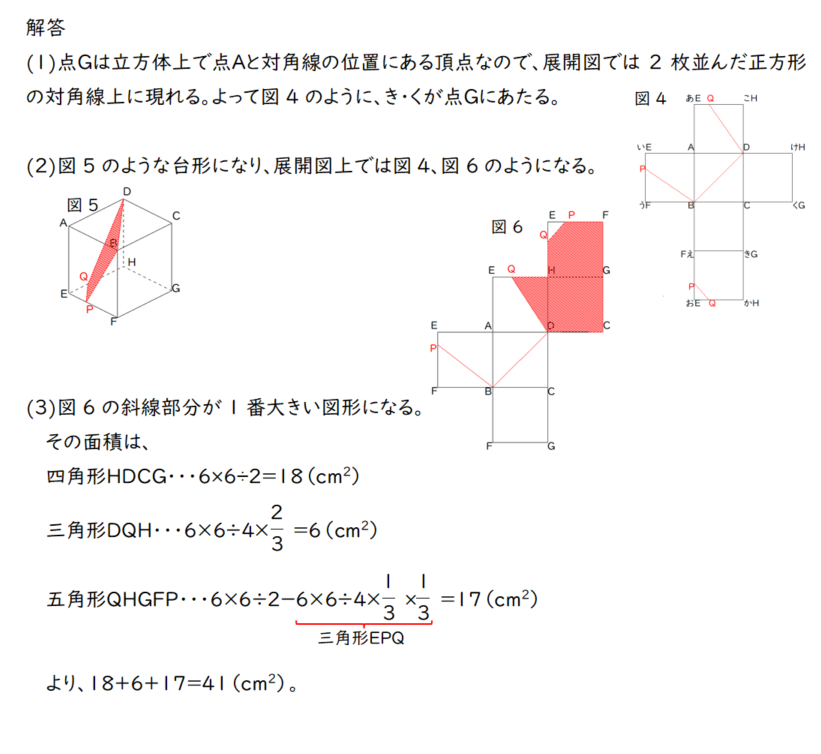
A.(1)き・く(2)解説参照(3)41cm2






ディスカッション
コメント一覧
まだ、コメントがありません