算数文章題講座 仕事算・ニュートン算の解き方 練習問題
仕事算・ニュートン算の練習問題 解説動画
仕事算の演習プリントはこちらをクリック
仕事算のオンラインテストはこちらをクリック
仕事算とニュートン算
仕事算は1人1人の仕事力と、全体の仕事量さえ決まればいいって話だったよね。

はるか

Haru_You
うん、試験で出る問題でもそこを押さえておけば解ける問題が多いよ。
多い、ってことはそうじゃない問題もあるってことだよね?

はるか

Haru_You
仕事を始めたあとに仕事が増加していくことで全体の仕事量が変化する問題、ニュートン算ってのがあるんだよ。
今回はそれを取り上げるんだ?

はるか

Haru_You
そうだね、前半はこれまでの仕事算の応用で、後半でニュートン算に入るよ。
もし、全仕事と仕事力の設定っていう、仕事算の基本を忘れたときは前回の基本問題を復習してね。
もし、全仕事と仕事力の設定っていう、仕事算の基本を忘れたときは前回の基本問題を復習してね。
途中で交代する仕事算の例題
ある仕事をするのに、A1人ですると15日、AとBの2人ですると10日かかります。この仕事をA1人ではじめ、途中からBに交代したところ全部で18日かかりました。Aは何日仕事をしましたか
この例題も、いつものように全体の仕事量と仕事力を決められるよね。
全体の仕事量が30、Aの仕事力が②で、AとBが③だから、Bの仕事力は①だね。
全体の仕事量が30、Aの仕事力が②で、AとBが③だから、Bの仕事力は①だね。

はるか

Haru_You
うん、そこまでOK。
これをAが最初に何日かやって、途中からBに代わって全部で18日だけど、どうしたらいいかわかるかな?
これをAが最初に何日かやって、途中からBに代わって全部で18日だけど、どうしたらいいかわかるかな?
えーと、全体の仕事量はわかってるんだから、Aが1日の場合、2日の場合・・・って日数を表に書いてって、あてはまるやつ探せばいいかなあ。

はるか

Haru_You
間違いではないけど・・・。
「全体の量」が決まっている問題では定番の解き方があったよね。
「全体の量」が決まっている問題では定番の解き方があったよね。
途中で交代する仕事算(仕事つるかめ)の解き方

そっか、つるかめ算を使えばいいのか。
仕事算で解くことばっかり考えていたよ。
仕事算で解くことばっかり考えていたよ。

はるか

Haru_You
仕事算っていうのは、全体の仕事量と個々の仕事力を出すまでの計算のことだからね。
その後がつるかめ算になる問題はすごいよく出るんだよ。
その後がつるかめ算になる問題はすごいよく出るんだよ。
こんなふうに仕事をする人が途中で交代するときが、つるかめ算になるのかな?

はるか

Haru_You
うん、交代したり休んだり、途中で仕事力が変化するときは仕事のつるかめ算で解くことが多いんだ。
ほら、途中で速さを変える文章題が、速さのつるかめ算になるのと同じだよ。
ほら、途中で速さを変える文章題が、速さのつるかめ算になるのと同じだよ。
3人組の仕事算の例題
A1人ですると30日、B1人ですると24日、C1人ですると20日かかる仕事があります。この仕事を1日目はAとB、2日目はBとC、3日目はCとA、4日目はまたAとB・・・という組み合わせの2人ずつですると、何日かかりますか
えーと、まずは仕事が終わる日数の逆比を取ればいいんだよね。

はるか

Haru_You
3つの量で逆比をとってもいいけど、分数にしないといけないからね。
3人の仕事算なら、仕事が終わる日数の最小公倍数を全体の仕事量にするほうが計算は楽だよ。
3人の仕事算なら、仕事が終わる日数の最小公倍数を全体の仕事量にするほうが計算は楽だよ。
たしかに。
そしたら全体の仕事量が120でAの仕事力が④、Bの仕事力が⑤、Cの仕事力が⑥だね。
あとはAとB、BとC、CとA・・・ってどう計算すればいいかなあ。
そしたら全体の仕事量が120でAの仕事力が④、Bの仕事力が⑤、Cの仕事力が⑥だね。
あとはAとB、BとC、CとA・・・ってどう計算すればいいかなあ。

はるか

Haru_You
周期で交替してるからね、周期算を使って考えるといいかな。
3人組の仕事算の解き方

今回は周期にしてぴったり割り切れたけど、割り切れない場合もあるよね?

はるか

Haru_You
その場合はあまりが残った仕事量だから、それを1日ずつ消化していけばいいんだよ。
3人組・途中で休む仕事算の例題
ある仕事をするのに、A1人では36日、B1人では45日、C1人では30日かかります。この仕事をA、B、Cの3人で始めましたが、途中でAが2日、Bが5日休みました。このとき、仕事が終わるまで全部で何日かかりますか
これも全体の仕事量とみんなの仕事力は求められるな。
3人のときは逆比より公倍数の方が楽なんだよね。
3人のときは逆比より公倍数の方が楽なんだよね。

はるか

Haru_You
うん、全体の仕事量は180、Aを⑤、Bを④、Cを⑥とするところまではいいよね。
あとはAとBが休まなかったとして3人で5+4+6=⑮だから・・・。
でも、つるかめ算にするには、全体の日数がわからないからなあ。
でも、つるかめ算にするには、全体の日数がわからないからなあ。

はるか

Haru_You
この問題はつるかめ算じゃないんだよね。
でも、他の和と差の問題で使ったことのある考え方で解けるんだよ。
でも、他の和と差の問題で使ったことのある考え方で解けるんだよ。
3人組・途中で休む仕事算の解き方

休んだぶんを休んでないことにして、仕事を増やしちゃうわけか。
で、3人で全部働いたと考えて、増えた全体の仕事を3人の仕事力で割るんだね。
で、3人で全部働いたと考えて、増えた全体の仕事を3人の仕事力で割るんだね。

はるか

Haru_You
これは算数文章題の鉄則、「よけいなはんぱ・例外はなくして考える」という解き方だね。
線分図でマル数字じゃないところを消したり、ダイコンを予定より2本多く買ったとかをなくしちゃうやつだね。
全体の日数がわかればつるかめで、全体の日数がわからないときは休まなかったことにすればいいんだね。
全体の日数がわかればつるかめで、全体の日数がわからないときは休まなかったことにすればいいんだね。

はるか

Haru_You
うん、問題の条件によって最後の計算は異なるけど、仕事力と全体の仕事量を求めるっていう仕事算の基本は共通だからね。
最初の量と増える量がわかるニュートン算・泉の例題
200Lの水がたまっている泉があり、この泉に毎分10Lの割合で水が湧き出しています。ポンプ1台でこの泉の水をくみ出すのに40分かかったとき、ポンプ2台で水をくみ出すのには何分かかりますか
200Lくみ出すっていう仕事をポンプでするんだよね。
ポンプの台数が2台に増えれば、くみだすのにかかる時間は減るかな。
ポンプの台数が2台に増えれば、くみだすのにかかる時間は減るかな。

はるか

Haru_You
うん、仕事算としてはそう考えるのが正しいね。
じゃあさ、1台で40分なんだから、2台にしたら逆比で20分になるんじゃないの?
ポンプ1台が1分に5Lずつくみ出すって計算になるし。
ポンプ1台が1分に5Lずつくみ出すって計算になるし。

はるか

Haru_You
この泉から水が湧いていなければそれでいいんだけど、この泉は1分ごとに水が増えていくからね。
1台が40分でくみ出す量と、2台が20分でくみ出す量は違うんだよ。
1台が40分でくみ出す量と、2台が20分でくみ出す量は違うんだよ。
そっか、これが仕事の増えていく仕事算ってやつなんだね。

はるか

Haru_You
うん、こんなふうに、時間とともに仕事が増えていく仕事算のことを、ここではニュートン算と呼ぶことにするよ。
で、ニュートン算はどうやって解いたらいいの?

はるか

Haru_You
ニュートン算で注目するのは、「はじめにある仕事量」と「時間ごとに増える仕事量」なんだ。
ここから、「見かけ上の仕事力」を求めていくんだよ。
ここから、「見かけ上の仕事力」を求めていくんだよ。
最初の量と増える量がわかるニュートン算・泉の解き方

はじめの量が200L、増える量が10Lってわかってるから実際にくみ出した量が200+10×40=600Lって計算して、1台の仕事力が600÷40=15Lになったんだよね。

はるか

Haru_You
うん、「はじめにある仕事量」と「時間ごとに増える量」から、実際の仕事力を取り出して、「見かけ上の仕事力」に直すわけだね。
初回の解説だからこういう解き方にしたけど、実は増えた仕事量の計算をしなくても「見かけ上の仕事力」が求められるんだよ。
だってさ、200Lを40分でくみ出してるんだよ。
初回の解説だからこういう解き方にしたけど、実は増えた仕事量の計算をしなくても「見かけ上の仕事力」が求められるんだよ。
だってさ、200Lを40分でくみ出してるんだよ。
そしたら、1分に200÷40=5Lが1台でくみ出したときの見かけ上の仕事力だよね。
あ、でも10L湧いてるのに5L減ってるんだから1台あたり15Lくみ出してるってわかるね。
こっちのほうが計算は簡単かな。
あ、でも10L湧いてるのに5L減ってるんだから1台あたり15Lくみ出してるってわかるね。
こっちのほうが計算は簡単かな。

はるか

Haru_You
もう1回、今度は見かけ上の仕事力を先に求める形で解いてみようか。
問題文のパターンも知っておいてほしいし。
問題文のパターンも知っておいてほしいし。
最初の量と増える量がわかるニュートン算・行列の例題
コンサート会場入り口に450人の人が行列をつくり、この行列に毎分15人が新たに並びます。窓口を2つ開くと6分で行列がなくなったとき、窓口1つでは行列がなくなるのに何分かかりますか
はじめから行列していて、そこに後から並ぶ人がいるから、仕事が増えていくニュートン算だね。

はるか

Haru_You
うん、行列が窓口に入っていく問題もニュートン算の定番だね、
さっきは増えた仕事量から計算してみたけど、今度は見かけ上の仕事力から先に計算してみよう。
さっきは増えた仕事量から計算してみたけど、今度は見かけ上の仕事力から先に計算してみよう。
450人が6分でいなくなったから、450÷6=75人/分、かな。
これが窓口2つの仕事力だよね。
でも、窓口1つだと75÷2=37.5人、ってことじゃないよね。
1分間に行列にならぶ人数を考えてないから。
これが窓口2つの仕事力だよね。
でも、窓口1つだと75÷2=37.5人、ってことじゃないよね。
1分間に行列にならぶ人数を考えてないから。

はるか

Haru_You
その通り。
ここで気をつけてほしいのは、「見かけ上の仕事力」では、仕事をする人数や台数が変わっても絶対にかけ算やわり算をしないこと。
必ず、1分に増えた仕事から実際の仕事力に直して、その上で人数や台数を変えるんだ。
ここで気をつけてほしいのは、「見かけ上の仕事力」では、仕事をする人数や台数が変わっても絶対にかけ算やわり算をしないこと。
必ず、1分に増えた仕事から実際の仕事力に直して、その上で人数や台数を変えるんだ。
最初の量と増える量がわかるニュートン算・行列の解き方

2つの窓口で見かけ上の仕事力が75人/分だから、実際の仕事力は75+15=90人/分ってことだよね。
それを2で割ると、1つの窓口の実際の仕事力が45人/分だ。
それを2で割ると、1つの窓口の実際の仕事力が45人/分だ。

はるか

Haru_You
その見かけ上の仕事力+仕事の増える量=実際の仕事力っていう計算がポイントだからね。
さっきのように全体の仕事量を計算するか、今のように見かけの仕事力から計算するかは好みの問題だから、自分でやりやすい方で練習してね。
さっきのように全体の仕事量を計算するか、今のように見かけの仕事力から計算するかは好みの問題だから、自分でやりやすい方で練習してね。
これでニュートン算はもう大丈夫かな?

はるか

Haru_You
まさか、この次が本番だよ。
「はじめにある仕事量」と「時間ごとに増える仕事量」に注目、って話したと思うんだけど、その2つがわからない状態から始まるニュートン算があるんだよ。
「はじめにある仕事量」と「時間ごとに増える仕事量」に注目、って話したと思うんだけど、その2つがわからない状態から始まるニュートン算があるんだよ。
仕事力だけわかるニュートン算の例題
ある量の水がたまっている池があり、この池には毎分一定の割合で水が流れ込んでいます。1分間に30Lの水をくみだすポンプを1台使うと、この池の水を全てくみ出すのに30分かかり、ポンプ4台で水を全てくみ出すのには5分かかるとき、はじめに池にたまっていた水の量は何Lですか
「はじめにある仕事量」がわからないから、見かけ上の仕事力は計算できないね。
「時間ごとに増える量」もわからないし、どうしたものかな。
「時間ごとに増える量」もわからないし、どうしたものかな。

はるか

Haru_You
このように仕事の終わる時間が2通りで、「はじめにある仕事量」と「時間ごとに増える量」についての条件が不足したニュートン算は、図を書いて解くんだよ。
どんな図を使うの?

はるか

Haru_You
ニュートン算を解くのに使うのは、線分図なんだよ。
実際に書いてみよう。
実際に書いてみよう。

仕事力だけわかるニュートン算の解き方
くみ出した全体の量が線の長さになってるんだね。

はるか

Haru_You
で、線分図の中で必ず「はじめにある仕事量」と「後から増えた仕事量」をわけるんだ。
はじめにある量はどちらも同じだけど、後から増えた量はくみ出した時間によって異なるから、全体の量(線分図の長さ)の差=あとから増えた量の差になるんだよ。
はじめにある量はどちらも同じだけど、後から増えた量はくみ出した時間によって異なるから、全体の量(線分図の長さ)の差=あとから増えた量の差になるんだよ。
今回の例でいえば、くみ出した全体の量の差300Lが、あとから増えた量の差になるんだよね。

はるか

Haru_You
で、あとから増えた量の差を、増えた時間の差で割れば「時間ごとに増える量」がわかるんだよ。
そこまで求めれば、あとははじめにあった量を計算するだけだね。
そこまで求めれば、あとははじめにあった量を計算するだけだね。
仕事力を①にするニュートン算・行列の例題
コンサート会場入り口に500人の人が行列をつくり、この行列に毎分決まった人数が新たに並びます。窓口を3つ開くと50分で、窓口を5つ開くと25分で行列がなくなったとき、窓口を6つ開くと、行列がなくなるのに何分かかりますか
この例題もニュートン算で、仕事の終わる時間が2通りになるから、線分図にするんだよね。
でもさ、さっきと違って1分間に何人の人が窓口から入れるかわからないから、全体の量を計算して線にできないよ。
でもさ、さっきと違って1分間に何人の人が窓口から入れるかわからないから、全体の量を計算して線にできないよ。

はるか

Haru_You
このようにニュートン算の線分図を書くときに、仕事力(減っていく量)の設定がないときは1分・1台あたりの仕事力を①に設定するんだ。
この問題なら窓口1つが1分に①人ずつ入れる、って考えてみるんだよ。
この問題なら窓口1つが1分に①人ずつ入れる、って考えてみるんだよ。
そうすると、3つの窓口50分でマル150、5つの窓口25分でマル125の人が入っていくから・・・

はるか

Haru_You
増えた=後から並んだ人がマルいくつだか、見えてきたでしょ。
仕事力を①にするニュートン算・行列の解き方

あれ、①あたりが何人だか求めてないのに問題解けちゃったね。

はるか

Haru_You
ここでは始めに並んでいたのがマル100あたり500人だから①あたり5人って求められるし、そこから1分間に並ぶ人数や1つの窓口から入れる人数も計算できるけどね。
試験でニュートン算が出るときは、そちらも合わせて聞いてくることが多いよ。
実際の人数を聞かれていようが、仕事が終わる時間を聞かれていようが、仕事力が決まらないニュートン算では仕事力を①にしてみればいいんだよ。
試験でニュートン算が出るときは、そちらも合わせて聞いてくることが多いよ。
実際の人数を聞かれていようが、仕事が終わる時間を聞かれていようが、仕事力が決まらないニュートン算では仕事力を①にしてみればいいんだよ。
仕事力を①にするニュートン算・牧場の例題
牧場に牧草が生えていて、牧草は毎日一定の量だけ増え、牛1頭が一定の量の牧草を毎日食べます。この牧場に牛を40頭放牧すると15日で、25頭放牧すると30日でちょうど牧草を食べ尽くします。この牧場で牧草がなくなる心配なしに放牧できる牛は、もっとも多くて何頭ですか
これもニュートン算なの?

はるか

Haru_You
うん、牧場に生える牧草とそれを食べる牛、っていうのはニュートン算の典型的な問題だよ。
この場合、1日に牧草が生える量と、牛が食べる量のどっちを①にするの?

はるか

Haru_You
ニュートン算は仕事算の1種だからね、「減っていく」ほうを仕事として考えるべきなんだ。
だから、牛1頭が1日に食べる牧草を①として考えるんだよ。
だから、牛1頭が1日に食べる牧草を①として考えるんだよ。
仕事力を①にするニュートン算・牧場の解き方
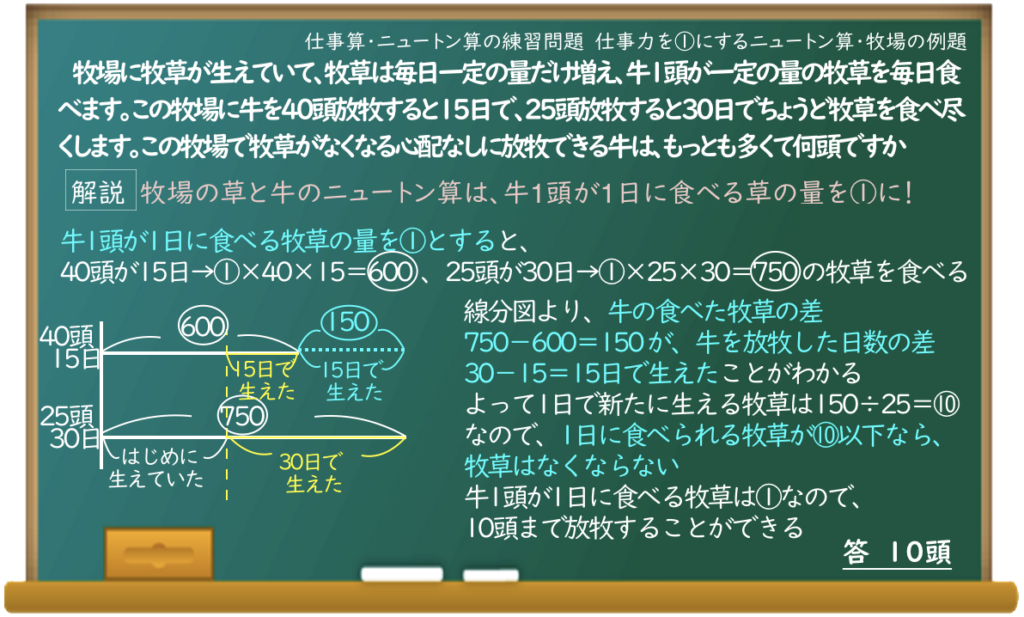
具体的な牧草の量とか全く考えずに、マル数字だけで計算しているんだね。

はるか

Haru_You
もし牛1頭が1日に10kg食べる、とか設定があればそれを組み合わせて計算すればいいだけだしね、さっきと同じだよ。
この問題も、例えば牛15頭なら何日でなくなるか、みたいな質問にできる?

はるか

Haru_You
1日に生える草が⑩って決まったから、はじめから生えていた牧草の量もマル数字で決まるでしょ。そしたら、見かけ上の仕事力を考えて計算すればいいだけだよ。
750−30×10=450がはじめの牧草で、15頭だと見かけ上の仕事力は15-10=になるから、450÷5=90日で牧草がなくなるね。

はるか
仕事算・ニュートン算の練習問題 まとめ
・途中で仕事をする人が交替するときは「仕事つるかめ」!
・3人の仕事算では、全仕事を終わる日数の最小公倍数に設定!
・仕事が時間ごとに増えていくニュートン算で注目するのは、「はじめにある仕事量」と「時間ごとに増える仕事量」!
・条件不足で計算できないニュートン算は、減っていく仕事を①にして線分図で表す!
仕事算・ニュートン算の練習問題 演習プリント
演習プリントには、Excelファイル版とPDFファイル版があります。
Excelファイル版はリロード・再計算(F8)するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
Excelファイル版はリロード・再計算(F8)するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。

はるか
仕事算・ニュートン算の練習問題
1 ファイル 145.83 KB
仕事算・ニュートン算の練習問題(PDF版)
1 ファイル 381.84 KB
利用規定です。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。

はるか











ディスカッション
コメント一覧
まだ、コメントがありません