平面図形の求積・角度（聖光学院　H24大問4改）

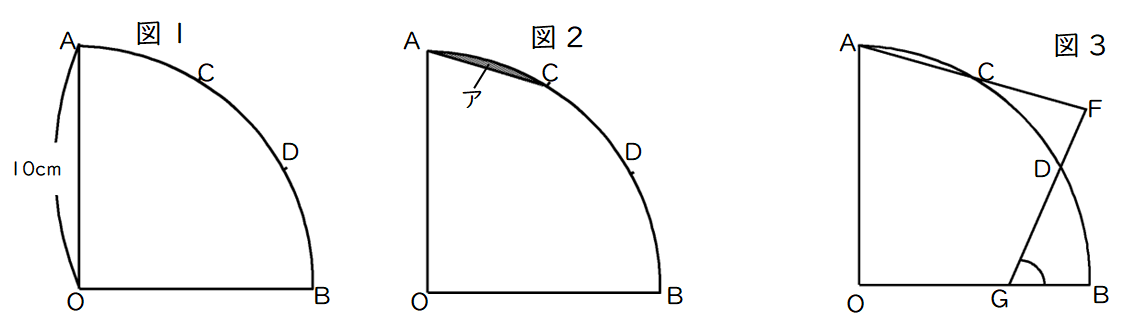
図1のように半径10cm、中心角90°のおうぎ形AOBがあり、おうぎ形の曲線ABの部分を3等分した点を、Aに近い方からC、Dとします。このとき、次の問いに答えなさい。ただし。円周率は3.14とします。

(1)図2のように点Aと点Cを直線で結んでできるアの部分の面積は何cm²ですか。
(2)図3のように点Aと点Cを結んだ直線の延長線上にAF＝10cmとなる点Fをとり、点Fと点Dを結んだ直線の延長線とOBとの交点をGとするとき、角BGDの大きさは何度ですか。

解法のポイント

折りたたみ可能コンテンツ

（1）は、四分円の弧の三等分ですから、30°のおうぎ形ができていることがわかります。
ここから三角形を引いた面積がアの部分ですが、頂角30°の二等辺三角形に三角定規をはめこむ解法は定番なので覚えておきましょう。
（2）の角度では、AF＝10cmの条件からOFに補助線を引き、二等辺三角形AOFを作ってみたくなりますが、それをやると手詰まりになります。おうぎ形内角度では正三角形がポイントになることが多いので、まずはOD、ADに補助線を引いて正三角形を作ってみましょう。