算数文章題講座 速さの3公式の解き方 練習問題
速さの練習問題 解説動画
速さの演習プリントはこちらをクリック
速さのオンラインテストはこちらをクリック
速さ、時間、道のりの公式など基本問題の解説はこちらをクリック
速さの文章題の考え方
速さの３公式はわかったつもりなんだけど、文章題になるといまいち答えがだせないんだよね。
はるか
Haru_You
それは問題文の読み方が下手なんだよ。
速さの文章題は「何を求めるか」じゃなくて、「問題の条件で何がわかっているか」から考えるんだ。
速さの文章題は「何を求めるか」じゃなくて、「問題の条件で何がわかっているか」から考えるんだ。
たとえば、問題の条件で速さと道のりがわかっていたら？
はるか
Haru_You
そしたら、道のり÷速さで時間を計算してから、その問題が聞いていることを求めるんだよ。
試しにやってみようか。
試しにやってみようか。
道のりと速さから求める例題
学校まで1.5kmの道のりを、いつもは60m/分で歩いて通っています。ある日、いつもより家を出るのが13分遅れたので自転車で行ったところ、いつもと同じ時刻に学校につきました。自転車の速さは毎分何mですか。
自転車の速さを求めるんだよね。
速さだから道のり÷時間で、道のりは学校まで1.5kmか。
えーと、13分遅れで出たって書いてあるけど、何分かかったかは書いてないんだなあ。
速さだから道のり÷時間で、道のりは学校まで1.5kmか。
えーと、13分遅れで出たって書いてあるけど、何分かかったかは書いてないんだなあ。
はるか
Haru_You
先に「何を求めるか」を気にしちゃうとそうなるよね。
ここでは、学校までの「道のり」といつもの「速さ」が与えられていることに注目するんだ。
ここでは、学校までの「道のり」といつもの「速さ」が与えられていることに注目するんだ。
「道のり」と「速さ」があったら時間が求められるよね。
あ、いつもは学校まで何分で行くかわかれば、13分遅れになったら何分かかって行くかもわかるね。
あ、いつもは学校まで何分で行くかわかれば、13分遅れになったら何分かかって行くかもわかるね。
はるか
道のりと速さから求める例題の解き方
いつも歩いてかかる時間が25分だってわかってれば、ある日の自転車は12分かかるってわかるね。
はるか
Haru_You
速さの問題で、速さ・時間・道のりのうち2つがわかっているのは問題を解くための誘導だからね。
残り1つを求めたうえで、問題を読むと解きやすくなるんだ。
今回なら、速さと道のりがわかっているんだから、道のり÷速さで時間を求めたわけだね。
残り1つを求めたうえで、問題を読むと解きやすくなるんだ。
今回なら、速さと道のりがわかっているんだから、道のり÷速さで時間を求めたわけだね。
「何を求めるか」より「何がわかっているか」に注目ってことだね。
はるか
道のりと時間から求める例題
6kmの山道を往復するのに、行きは上り坂を1時間40分かけて上りましたが、帰りは下り坂だったので行きより分速が15m速くなりました。帰りにかかった時間は何時間何分ですか
求めるのは帰りにかかった時間だけど･･･。
はじめに、行きは6kmの道のりを1時間40分かかったって書いてあるね。
そこで道のり÷時間で行きの速さを求めちゃえば、帰りの速さもわかるし、そこから計算するってことだね。
はじめに、行きは6kmの道のりを1時間40分かかったって書いてあるね。
そこで道のり÷時間で行きの速さを求めちゃえば、帰りの速さもわかるし、そこから計算するってことだね。
はるか
Haru_You
うん、それでOK。
速さの文章題は考えるより、求められるものを先に計算、が鉄則だね。
速さの文章題は考えるより、求められるものを先に計算、が鉄則だね。
他の問題はどうだっけ？
はるか
Haru_You
和と差の問題のときは何算だか考えるのが大事だし、整数の問題は規則性を見つけるのが先決になるかな。
道のりと時間から求める例題の解き方
いったん単位を直して、上りの速さを分速にしたのは、最後に「何時間何分」で求めるから？
はるか
Haru_You
それよりも、時速で計算して上りの3.6km/時に15m/分＝0.9km/時をたすほうが計算が面倒だからだね。
解答の単位は最後に直せば済むから、計算途中でミスの出やすくなるような数字で計算するのを避ける方がいいかな。
解答の単位は最後に直せば済むから、計算途中でミスの出やすくなるような数字で計算するのを避ける方がいいかな。
問題全体を見ながら単位を考えていく必要があるんだね。
はるか
速さと時間から求める例題
分速150mで24分かかる道のりを、時速4㎞で進むと何分かかりますか
もうこのパターンはお腹いっぱいだよ。
今度は速さと時間が書いてあるから、先に道のりを先に求めておくんでしょ。
で、時速4kmで割ってあげればいいんじゃん。
今度は速さと時間が書いてあるから、先に道のりを先に求めておくんでしょ。
で、時速4kmで割ってあげればいいんじゃん。
はるか
Haru_You
3問続くと、さすがにパターン覚えてくれるね。
速さと時間から求める例題の解き方
後半で出てくるのが時速4kmで、分速にしちゃうと分数になるから、道のりをkmに直して計算したんだね。
だいたい解き方のパターンが見えてきたなあ。
だいたい解き方のパターンが見えてきたなあ。
はるか
Haru_You
ところで、この問題には全く別の解き方もあってね。
分速150mってさ、時速9kmじゃん。
時速9kmと時速4kmだったらどっちが時間かかると思う？
分速150mってさ、時速9kmじゃん。
時速9kmと時速4kmだったらどっちが時間かかると思う？
当然、時速4kmの方が遅いから、そっちのが時間はかかるよね。
はるか
Haru_You
じゃあ、これを比にしてみようか。
速さが時速9km：時速4kmで9：4だろ。
9km/時のとき24分でさ、4km/時では54分って答えが出たけど、これって時間は24分：54分＝4：9になるってことだよね。
速さが時速9km：時速4kmで9：4だろ。
9km/時のとき24分でさ、4km/時では54分って答えが出たけど、これって時間は24分：54分＝4：9になるってことだよね。
あ、逆比になってるんだね。
はるか
Haru_You
うん、これは次の「速さと比」って単元で取り上げるけど、速さの問題は比を使って解くこともあるから、解き方の見極めが重要になってくるんだよ。
平均の速さの例題
8kmの道のりを行きは毎時4kmで、帰りは毎時6kmで往復したときの、平均の速さは毎時何kmですか
行きが4km/時で帰りが6km/時なんだから、平均は（４+６）÷2＝5km/時じゃないの?
はるか
Haru_You
それじゃ、平均の速さじゃなくて速さの平均だよ。
まあ、これは「平均の速さ」って日本語が悪いんで、みんな苦手にしている問題なんだけどね。
ほら、問題文には「道のり」と「速さ」が書いてあるだろ。
まあ、これは「平均の速さ」って日本語が悪いんで、みんな苦手にしている問題なんだけどね。
ほら、問題文には「道のり」と「速さ」が書いてあるだろ。
えーと、これで行きにかかった時間と、帰りにかかった時間を求めることができるな。
往復でかかった時間がわかるから･･･
往復でかかった時間がわかるから･･･
はるか
Haru_You
うん、その考え方であってるよ。
「平均の速さ」は「往復全体の速さ」って言い換えると間違わないんだけどね。
ちょっと解いてみようか。
「平均の速さ」は「往復全体の速さ」って言い換えると間違わないんだけどね。
ちょっと解いてみようか。
平均の速さの例題の解き方
平均の速さって、速さを平均したものじゃなくって往復全体での速さのことなんだね。
はるか
Haru_You
うん、だから平均の速さ＝往復全体の道のり÷往復にかかった時間、なんだよ。
往復全体の道のりは片道の2倍で、往復にかかる時間は片道ごとに、問題文に書いてある道のりと速さから求めればいいんだ。
往復全体の道のりは片道の2倍で、往復にかかる時間は片道ごとに、問題文に書いてある道のりと速さから求めればいいんだ。
でも、この問題途中で分数になって計算が面倒だね。
はるか
Haru_You
これは裏技なんだけど、この問題の道のりを12kmにして計算するとどうなるか求めてみな。
えっと、道のり12kmだと、行きが12÷4=3時間、帰りが12÷6=2時間だね。
往復で12×2=24kmの道のりを3+2=5時間だから、平均の速さは24÷5=4.8km/時かな。
あれ、さっきと一緒だ。
往復で12×2=24kmの道のりを3+2=5時間だから、平均の速さは24÷5=4.8km/時かな。
あれ、さっきと一緒だ。
はるか
Haru_You
往復の平均の速さは道のりの長さに関係なく、行きと帰りの速さが決まれば一定になるんだ。
そこで平均の速さを求めるときには道のりを行き帰りの速さの最小公倍数にして計算することができるんだよ。
そこで平均の速さを求めるときには道のりを行き帰りの速さの最小公倍数にして計算することができるんだよ。
途中で速さを変える例題
家から1200m離れた郵便局へ行くのに、途中まで分速140mで走り、途中から分速60mで歩いたところ、ちょうど12分で郵便局に着きました。走った道のりは何mですか
問題が聞いているのは走った道のりだけど･･･。
道のりも速さも時間も書いてあるから、どれを組み合わせたらいいのかなあ。
道のりも速さも時間も書いてあるから、どれを組み合わせたらいいのかなあ。
はるか
Haru_You
この問題は特殊な解き方をする問題なんだ。
どこで見分けるかというと、ある道のりを進む間に速さを変えるという設定だね。
どこで見分けるかというと、ある道のりを進む間に速さを変えるという設定だね。
たしかに、途中まで140m/分で進んでたのに、途中から60m/分に変えてるね。
はるか
Haru_You
こんなふうに道のりの長さがわかっていて、途中で速さを変えるときは「速さのつるかめ算」に持ち込むんだ。
まずは解いてみようか。
まずは解いてみようか。
途中で速さを変える例題（速さつるかめ）の解き方
歩いた時間と走った時間の合計12分ってところから、12分全部歩いたことにするとつるかめ算になるんだね。
はるか
Haru_You
うん、速さのつるかめ算は「全ての時間を一方の速さで進んだときに進む道のり」を考えて、実際の道のりとの差÷速さの差＝もう一方の速さで進んだ時間、を求めるんだ。。
この問題みたいに、道のりを求めるときでも、道のりの差÷速さの差＝時間を求めるのね。
はるか
Haru_You
うん、速さのつるかめ算では「全ての時間を一方の速さで進んだときに進む道のり」を考えて、実際の道のりとの差÷速さの差＝もう一方の速さで進んだ時間、を求めるんだ。。
到着時刻が前後する例題
学校へ登校するのに毎朝8時10分に家を出て、100m/分で歩いていくと始業時刻の3分前に学校に着き、60m/分で歩いて行くと始業時刻の5分後に学校に着きます。始業時刻は8時何分ですか
えっと･･･速さは書いてあるけど道のりが書いてないから、式が立てられないなあ。
はるか
Haru_You
そうだね。
だからこの問題は比を使って解くこともあるんだけど、ここでは速さの3公式で解く方法でやってみよう。
この問題で注目するポイントは、同じ道を2通りの速さで行くとき、「決められた時刻に到着時刻が前後する」ことだね。
だからこの問題は比を使って解くこともあるんだけど、ここでは速さの3公式で解く方法でやってみよう。
この問題で注目するポイントは、同じ道を2通りの速さで行くとき、「決められた時刻に到着時刻が前後する」ことだね。
うん、100m/分なら間に合うし、60m/分だと遅刻しちゃうんだよね。
はるか
Haru_You
こんなふうに、2通りの速さで到着が指定時刻に前後するときは、速さの差集め算を使うんだ。
実際に解いてみるから、よく見ててね。
実際に解いてみるから、よく見ててね。
到着時刻が前後する例題（速さ差集め）の解き方
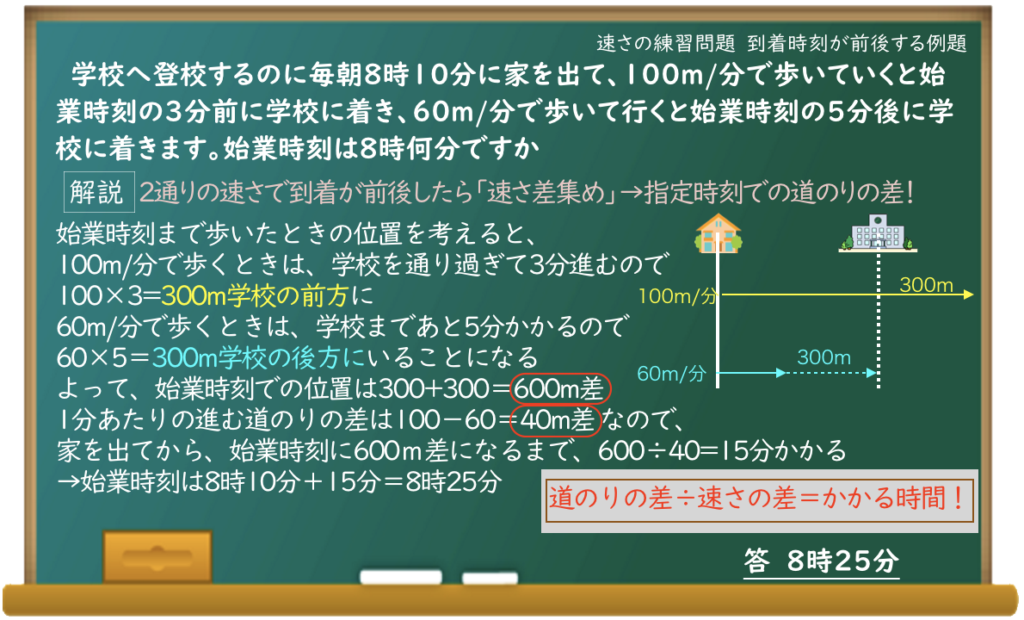
3分前に着くなら、始業時刻には学校を通り過ぎてる、っておもしろいね。
はるか
Haru_You
始業時刻まで歩いたときの位置でそろえたいからね。
速さの差集め算は、指定時刻まで進んだときの道のりの差÷速さの差＝指定時刻までの時間、っていう計算になるんだよ。
速さの差集め算は、指定時刻まで進んだときの道のりの差÷速さの差＝指定時刻までの時間、っていう計算になるんだよ。
この問題で、学校までの道のりを聞かれたらどうするの？
はるか
Haru_You
100m/分だと始業の3分前、8時22分に着くんだから12分かかるわけだよね。
だから、100×12=1200mって求めればいいんだ。
何を聞いていようが、この問題では差集めに持ち込んで、そこから解いていくよ。
だから、100×12=1200mって求めればいいんだ。
何を聞いていようが、この問題では差集めに持ち込んで、そこから解いていくよ。
速さの練習問題 まとめ
・速さの文章題は、「何を求めるか」の前に「何がわかっているか」から！
・「平均の速さ」＝合計の道のり÷合計の時間！
・道のりの途中で速さを変えたら「速さつるかめ」、道のりの差÷速さの差！
・到着時刻が前後したら「速さ差集め」、道のりの差÷速さの差！
速さの練習問題 演習プリント
演習プリントには、Excelファイル版とPDFファイル版があります。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
はるか
速さの練習問題（PDF版）
1 ファイル 329.55 KB
利用規定です。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
はるか
新着記事
都立中高一貫校のHPで公開されている適性検査問題の作文（適性検査Ⅰ）を1つのPD ...
社会科、日本の歴史の各時代の重要事項を「アルプス一万尺」に乗せて歌います。。
中学受験理科講座 植物のつくりとはたらき(3)〜光合成・呼吸・蒸散〜
理科の生物範囲、植物のつくりとはたらきについて、光合成・呼吸・蒸散のはたらきにつ ...
中学受験で頻出の11種類の水溶液の名前、液性、指示薬の変化、主な水溶液の識別ポイ ...
コロナウイルスの影響で、中学受験の学習塾業界にも営業自粛要請が出ています。この状 ...