算数文章題講座 消去算の解き方 基本問題
消去算の演習プリントはこちらをクリック
消去算のオンラインテストはこちらをクリック
消去算って？
Haru_You
この消去算という単元は、「最小公倍数」が必要になっているので塾カリキュラムでは5年生になってから習うんだけど、そこを除けば小学3年生から解ける易しい文章題なんだよね。
どんな文章題が消去算なの？
はるか
Haru_You
消去算といえば「2種類の品物をそれぞれ個数を変えて買ったときの2通りの代金」っていう買い物の問題が基本パターンだね。
今回はそのタイプの問題をやってみるよ。
今回はそのタイプの問題をやってみるよ。
個数がそろった消去算の例題
みかん2個とりんご5個を買うと870円で、みかん2個とりんご3個を買うと570円です。みかん1個のねだんは何円ですか
なるほど、たしかに570円と870円で「2種類の品物をそれぞれ個数を変えて買ったときの2通りの代金」だ。
はるか
Haru_You
じゃあ、代金が2通りあったら何に注目したらいいと思う？
えーと、代金のちがい、かな？
はるか
Haru_You
そのとおり、文章題を解くとき大事な視点は「差に注目」することだからね。
じゃあ、なんで代金にちがいができてるんだか考えてみな。
じゃあ、なんで代金にちがいができてるんだか考えてみな。
だって、買った個数が違うじゃん･･･って、あれ？
どっちの買い方でもみかんは2個で一緒だから･･･
どっちの買い方でもみかんは2個で一緒だから･･･
はるか
Haru_You
うん、その考え方であってるから、ちょっと絵にしてみよう。
今回は解説のために絵にするけど、実際に解くときには絵は描かないでね。
今回は解説のために絵にするけど、実際に解くときには絵は描かないでね。
個数がそろった消去算の解き方
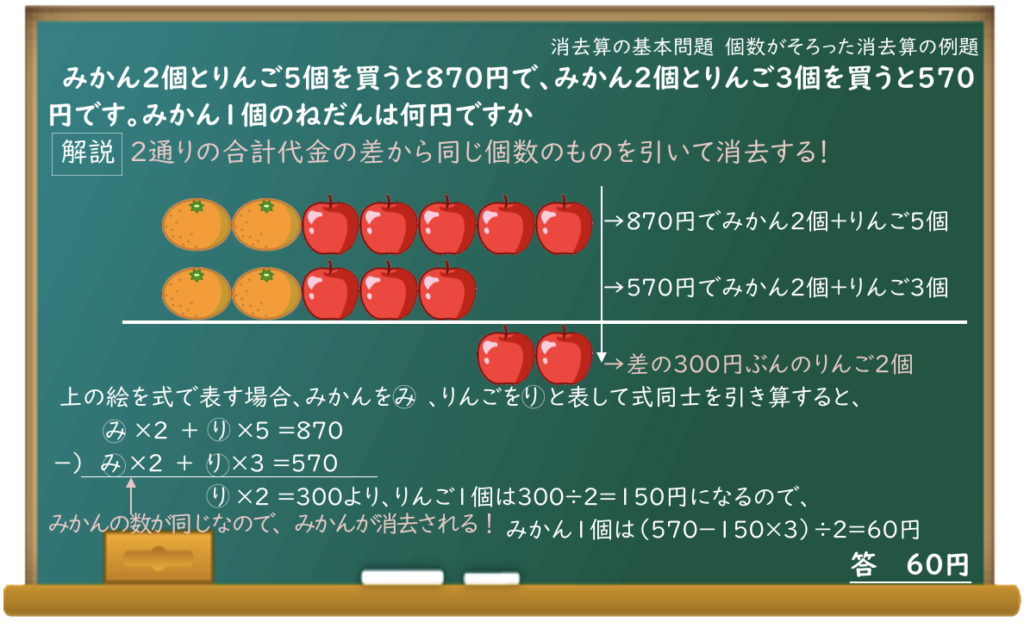
みかんの数が一緒だから、差の300円にみかんは関係ないんだよね。
だからりんごだけの差、2個分が300円ってことか。
だからりんごだけの差、2個分が300円ってことか。
はるか
Haru_You
うん、それでりんご1個の値段が求められるよね。
片方が求められれば、もう一方はどちらの式に当てはめても求められるから、簡単に計算できそうなほうで計算すればいいよ。
片方が求められれば、もう一方はどちらの式に当てはめても求められるから、簡単に計算できそうなほうで計算すればいいよ。
2つの買い方から、みかんを消して考えたから消去算っていうのかな。
はるか
Haru_You
その通り。
一方の品物の数がそろってれば、差を求めて引き算したときに消えるから、消去算という名前がついているんだ。
一方の品物の数がそろってれば、差を求めて引き算したときに消えるから、消去算という名前がついているんだ。
あれ、じゃあどっちかの品物は同じ数買ってないと、消去算は使えないってこと？
はるか
Haru_You
まさか。次は個数のそろわない消去算をやってみようか。
個数がそろわない消去算の例題
おにぎり2個とパン3個を買うと780円で、おにぎり4個とパン7個を買うと1740円です。おにぎり1個のねだんは何円ですか
おにぎりもパンも個数がそろわないから、引き算して960円差にしてもよくわからないよ。
はるか
Haru_You
そんなときは、どちらかの個数をそろえるように買うんだよ。
でも、おにぎりもパンもバラ売りしてないから、そろえられないよ。
はるか
Haru_You
うん、だからセットのまま買って個数をそろえるんだよ。
おにぎり2個とパン3個のセットを2セット買うとどうなるかな？
おにぎり2個とパン3個のセットを2セット買うとどうなるかな？
おにぎり4個とパン6個になるね。
で、780×2＝1560円か。
あ、これで前の例題と同じように解けるね。
で、780×2＝1560円か。
あ、これで前の例題と同じように解けるね。
はるか
Haru_You
うん、どっちがそろえやすいか、よく見てセット買いすればいいってことだ。
個数がそろわない消去算の解き方
Haru_You
セットで買うときに、代金も2倍なりなんなり、増やすのを忘れないようにね。
この問題でさ、パンの数をそろえて消去することできないかな？
そうすればすぐにおにぎり1個の値段が求められるじゃん。
はるか
Haru_You
う～ん、最初の買い方を7セット、2番目の買い方を3セット買えばパン21個でそろうけど、計算が面倒かな。
とはいえ、そんな場合もあるからやってみよう。
とはいえ、そんな場合もあるからやってみよう。
公倍数でそろえる消去算の例題
ガム2個とチョコ3個を買うと520円で、ガム5個とチョコ4個を買うと880円です。ガム1個のねだんは何円ですか
あ～、ガムもチョコもうまくそろえられないね。
でも最初のを5セット、2番目のを2セット買えばガムが10個になるのはなんとなくわかるな。
でも最初のを5セット、2番目のを2セット買えばガムが10個になるのはなんとなくわかるな。
はるか
Haru_You
そこはなんとなく、じゃなく「最小公倍数で個数をそろえる」という発想になってください。
だったらチョコは3と4の最小公倍数で12個にすればいいってことか。
でも、チョコとガムのどっちをそろえればいいの？
でも、チョコとガムのどっちをそろえればいいの？
はるか
Haru_You
消去算でそろえるのは好きなほうでいいんだけど、基本的には計算が楽そうなほうだね。
あと、そろえたほうが消えるから、どっちか一方だけ求めるときは、いらないほうでそろえれば少し楽かな。
あと、そろえたほうが消えるから、どっちか一方だけ求めるときは、いらないほうでそろえれば少し楽かな。
じゃあ、この場合はガムを求めるからチョコ12個にそろえて計算だね。
はるか
公倍数でそろえる消去算の解き方
Haru_You
今はガムを求めるためにチョコをそろえて消去したけど、場合によっては求めるやつでそろえてもう一方を出してから計算したほうが速いこともあるし、たくさん解いて臨機応変に使えるようにね。
これができれば、もう2種類の品物についての消去算は完璧だよね。
次は3種類の消去算でもやる？
次は3種類の消去算でもやる？
はるか
Haru_You
いやいや、消去算は他のタイプもあるのよ。
今やったのが「加減法型」っていうんだけど、「代入法型」ってのもあるんだ。
3種類の消去算はあとで取り上げるから、次は代入法型消去算ね。。
今やったのが「加減法型」っていうんだけど、「代入法型」ってのもあるんだ。
3種類の消去算はあとで取り上げるから、次は代入法型消去算ね。。
1つだけ交換する代入消去算の例題
えんぴつ3本とボールペン1本を買うと290円で、ボールペン1本のねだんはえんぴつ1本のねだんより50円高いとき、えんぴつ1本のねだんは何円ですか
セットの買い方が1種類しかないね。
そのかわり品物の値段の差がわかってるんだ。
ボールペンの方が50円高いんだね。
そのかわり品物の値段の差がわかってるんだ。
ボールペンの方が50円高いんだね。
はるか
Haru_You
えんぴつ3本とボールペン1本で290円ってことだけど、これをえんぴつだけの買い物にするよう、ボールペンを消去したいんだ。
そのためにはどうしたらいいと思う？
そのためにはどうしたらいいと思う？
え～と、ボールペンを1本返品して、えんぴつ1本に取っ替えてもらえばいいかな。
そのとき、代金は安くなるよね。
そのとき、代金は安くなるよね。
はるか
Haru_You
それで正解。
取っ替えてもらうときの処理が「代わりに入れる」から「代入」っていうんだ。
あとは代入時の代金の変化に気をつけて式にすれば、解けたも同然だよ。
取っ替えてもらうときの処理が「代わりに入れる」から「代入」っていうんだ。
あとは代入時の代金の変化に気をつけて式にすれば、解けたも同然だよ。
1つだけ交換する代入消去算の解き方
式の中でみると、○え×4+50＝290円から、290－50で240円にするってのがわかりにくいな。
安い方買ったから安くするのはわかるんだけど。
安い方買ったから安くするのはわかるんだけど。
はるか
Haru_You
線分図でやった、○のついてないはんぱな量をなくすって発想で考えればいいんだよ。
数学では=の反対側にたし算、引き算を動かすときに計算が逆になることを「移項」という言葉で説明するんだけど、知らなくても大丈夫。
数学では=の反対側にたし算、引き算を動かすときに計算が逆になることを「移項」という言葉で説明するんだけど、知らなくても大丈夫。
これ、ボールペンが2本だったら2本分、50×2＝100円安くすればいいんだよね？
はるか
Haru_You
うん、○ぼ×2＝○え×2+100の代入になるね。
そんなふうに、個数をそろえてから代入する消去算をやってみようか。
そんなふうに、個数をそろえてから代入する消去算をやってみようか。
個数をそろえて代入する消去算の例題
プリン3個とケーキ5個を買うと2350円で、ケーキ1個のねだんはプリン2個のねだんより50円安いとき、ケーキ1個のねだんは何円ですか
ケーキを求めたいからプリンを消去したいけど、プリンをケーキに取りかえてもらえうのはむずかしいなあ。
はるか
Haru_You
それなら、先にプリン1個の値段を求めてから計算すればいいだけだよね。
消去算ではどっちを求めるかより、計算しやすいほうから出すことが大事。
消去算ではどっちを求めるかより、計算しやすいほうから出すことが大事。
じゃあ、ケーキ1個がプリン2個と交換できるから、ケーキ5個はプリン10個と交換できるよね。
でもケーキの方が安いんだから、交換してもらうと代金は高くならないといけないんだよね。
でもケーキの方が安いんだから、交換してもらうと代金は高くならないといけないんだよね。
はるか
Haru_You
そうだね、そのときの代金の変化に気をつけて式を作ってみよう。
個数をそろえて代入する消去算の解き方
50円安い×5個ぶんで250円安いことになるんだね。
プリンのほうが安いから引きたくなるけど、プリン2個のほうが高いからたすんだよね。
ややこしくなるなあ。
プリンのほうが安いから引きたくなるけど、プリン2個のほうが高いからたすんだよね。
ややこしくなるなあ。
はるか
Haru_You
高い安いで考えるんじゃなくて、○数字から見たはんぱを消す、だからね。
消去算で一番ミスが多いのはこの処理なので、イメージだけで考えずに落ち着いて式を見るんだよ。
消去算で一番ミスが多いのはこの処理なので、イメージだけで考えずに落ち着いて式を見るんだよ。
これで消去算の基本問題はおしまい？
はるか
Haru_You
うん、条件を増やしたり買い物じゃなかったり、いろんな消去算があるから、それは練習問題で扱うよ。
消去算の基本問題 まとめ
・「2種類の品物をそれぞれ個数を変えて買ったときの2通りの代金」から、品物の値段を求めるのが消去算！
・一方の品物の個数をそろえて消去すれば、もう一方の品物の個数の差が代金の差になるのが加減法！
・一方の品物を、もう一方と取り替えて消去するのが代入法！
消去算の基本問題 演習プリント
演習プリントには、Excelファイル版とPDFファイル版があります。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
Excelファイル版はリロード・再計算（F8）するたびに数字や配列が変わります。
マクロは使用していませんので、セキュリティ警告はありません。
はるか
消去算の基本問題（PDF版）
1 ファイル 369.48 KB
利用規定です。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
本配布ファイルは個人利用に限り自由に使用することができますが、著作権は放棄していません。
学習塾、家庭教師などの商用利用は作成者までご相談ください。
本配布ファイルを利用した事によるいかなる損害も作成者は一切の責任を負いません。
はるか
新着記事
都立中高一貫校のHPで公開されている適性検査問題の作文（適性検査Ⅰ）を1つのPD ...
社会科、日本の歴史の各時代の重要事項を「アルプス一万尺」に乗せて歌います。。
中学受験理科講座 植物のつくりとはたらき(3)〜光合成・呼吸・蒸散〜
理科の生物範囲、植物のつくりとはたらきについて、光合成・呼吸・蒸散のはたらきにつ ...
中学受験で頻出の11種類の水溶液の名前、液性、指示薬の変化、主な水溶液の識別ポイ ...
コロナウイルスの影響で、中学受験の学習塾業界にも営業自粛要請が出ています。この状 ...